【Astro Advent Calendar2022 12/11】2022年12月の火星最接近と衝

こんにちは、あるいはこんばんは。おさむです。今月の天文トピックといえば約2年2ヶ月ぶりの火星の最接近ですね。少し気になることがあったので、軌道計算して確認してみました。

最接近する日と一番明るい日は別らしい
軌道計算で今回の火星最接近を再現してみる
おわりに
執筆者紹介
この記事はAstro Advent Calendar 2022の企画記事です。

最接近する日と一番明るい日は別らしい

火星の最接近は12月1日、一方で火星がもっとも明るく輝く日は12月6日から9日頃です。

ものは近いほど大きく見えますから、火星だって最接近する日に一番明るくなりそうな気がしますが、そうではないようです。

その理由について、国立天文台のほしぞら情報は以下のように説明されています。

惑星などの天体（この場合は火星）では、一般的に接近距離が近くなるほど明るくなる傾向にありますが、距離があまり変わらない場合には、衝の付近でより明るくなります。これを「衝効果」と言います。今回の火星の明るさは、最接近時がマイナス1.9等なのに対し、衝付近ではマイナス2.0等となります。
国立天文台、『火星が見頃、月が火星に接近（2022年12月）』、https://www.nao.ac.jp/astro/sky/2022/12-topics03.html

「衝」とは惑星が地球から見て太陽とちょうど反対の位置にくることです。惑星は楕円軌道を描き、太陽からの距離が時間とともに変動するため（火星は離心率 $e \sim 0.1$ の楕円軌道です）、衝と最接近は必ずしも一致しないのです。

それにしても、「衝効果」と呼ばれる現象は初耳でした。Wikipediaによると、

衝効果（しょうこうか、英語: opposition surge）とは、新井表面や多数の粒子に覆われた天体が観測者の真後ろから照らされた時に明るさが増す現象のことである。
Wikipedia『衝効果』、https://ja.wikipedia.org/wiki/%E8%A1%9D%E5%8A%B9%E6%9E%9C、2022年12月12日閲覧

と説明されています。満月がひときわ明るく輝くのも衝効果によるものだそうです。物理的な要因は「影が隠される効果」「干渉性後方散乱」の2つがあり、どちらが重要かは決着していないようです。それにしても、今月の火星の場合はマイナス1.9等からマイナス2.0等まで、光量にして10パーセントも明るくなっています。これには驚きました。

軌道計算で今回の火星最接近を再現してみる

（※本記事のように自分で軌道要素を調べて計算することはおすすめしません。天文学に関する数値計算・データ解析はpythonライブラリが充実しており、それらを利用すべきだからです。私もコードデバッグをしていたら執筆締切を過ぎてしまいました。各位申し訳ありません……）

見出しの通り、軌道を計算してみましょう。

惑星の軌道計算

NASAのサイトに Approximate Positions of the Planets というページがあって、太陽系に属する惑星の軌道要素と、おおまかな位置の計算方法が記されています。今回はここにしたがい計算してみます。

import numpy as np
import matplotlib.pyplot as plt

from table import table # 軌道要素のテーブル
from numkepler import numericalKeperE # Kepler方程式をNewton-Laphson法で解く
from orbit import R_x, R_y, R_z # x, y, z 軸周りの回転行列

class Orbital():
    def __init__(self, name, JED):
        # input 説明: name=惑星の名前, JED=軌道を計算したい時刻のnumpy配列
        self.paras = dict()
        # step 1: 軌道要素をテーブルから読み込む
        T = (JED - 2451545.)/36525.
        for k, v in table[name]:
            self.paras[k] = v['value'] + v['dot'] * T
            if v['unit'] == 'deg':
                self.paras[k] *= np.pi / 180 # すべてラジアンで記述
        # step 2
        self.paras['omega'] = self.paras['long.peri.'] - self.paras['long.node.']
        self.paras['M'] = self.paras['L'] - self.paras['long.peri.']
        # step 3: ケプラー方程式を数値的に計算し eccentric anomaly を求める
        self.paras['E'] = numericalKeplerE(M=self.paras['M'], epsilon=self.paras['e'])
        # step 4: 軌道座標での位置計算
        x_dash = self.paras['a'] * (np.cos(self.paras['E']) - self.paras['e'])
        y_dash = self.paras['a'] * np.sqrt(1-self.paras['e']**2) * np.sin(self.paras['E'])
        z_dash = np.zeros_like(x_dash)
        # step 5: 赤道座標への変換
        r_dash = np.array([x_dash, y_dash, z_dash])
        self.paras['r_ecl'] = R_z(self.paras['Omega'][0]) @ R_x(self.paras['I'][0]) @ R_z(self.paras['omega'][0]) @ r_dash
        self.paras['r_eq'] = R_x(23.44 * np.pi/180) @ self.paras['r_ecl']

惑星の赤道座標での位置を計算するクラス Orbital をつくってみました。呼び出すときは以下のようにします：

JED = np.linspace(2459905, 2459925, 21) # 11月21日から12月11日まで、毎日日本時間21時
mars = Orbital(name='Mars', JED = JED) # 毎日21時の火星の位置
earth = Orbital(name='EM Bary', JED = JED) # 地球(実は地球-月の共通重心)の位置

その他さまざまなメソッドをクラスに持たせたかったのですが、今回は時間の都合により断念。必要な関数はベタ書きしていきました。

def norm(vec):
    r = np.sqrt(np.sum(vec**2, axis=0))
    return vec / r

def stereo_projection(norm_vec, center_vec):
    # 球面上のベクトルを平面に射影する
　　　　# input 説明: norm_vec=射影したい位置ベクトルの配列, center_vec=射影の中心にするベクトル
    # step 1: 射影中心が'南極'に位置するよう回転
    cener_theta, center_phi = np.arcsin(center_vec[2]), np.arctan(center_vec[1]/center_vec[0])
    rotated_vec = R_y(center_theta + np.pi/2) @ R_z(-center_phi) @ norm_vec
    # ステレオ射影
    X = -rotated_vec[1] / (1 - rotated_vec[2])
    Y = rotated_vec[0] / (1 - rotated_vec[2])
    return (X, Y)

（参考：Wikipedia）

if __name__ == "__main__":
    JED = np.linspace(2459735, 2460095, 361) # 12月1日の前後180日ずつ、毎晩21時の時刻の配列
    embary = Orbital(name='EM Bary', JED=JED)
    mars = Orbital(name='Mars', JED=JED)

    vec_em = mars.paras['r_eq'] - embary.paras['r_eq'] # 地球から見た火星の位置

    norm_vec, r = norm(vec_em)
    X, Y = stereo_projection(norm_vec, norm_vec[:, 180])

これで火星の見かけの位置が計算できました。スクリプトをなくしちゃったのでどうやったか忘れましたが、プロットするとこのようになりました。

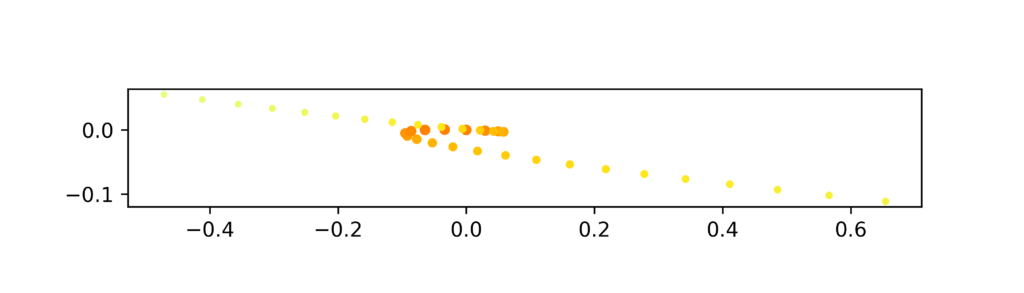
火星が右下からやってきて、そして逆行し、また左上へ抜けていく様子がわかります。逆行という（古代の人々にとっては）不可思議な現象が、楕円軌道の計算で確かに現れることが確認できました。

火星の明るさについて

惑星の明るさを決める重要な要素は3つあります。

惑星と地球の距離：遠ければ遠いほど小さく見えるので暗くなり、反対に近いほど大きく見えるので明るくなります。
惑星と太陽の距離：惑星は自分で輝きません。太陽の光を反射して光っています。したがって、太陽に近いほど素で明るくなります。
位相角（太陽-惑星-地球がなす角）：月の満ち欠けのようなもので、三日月は位相角が大きいから暗く、満月は明るいといったように、位相角は重要なパラメータです。
反射率：極端な話、真っ白な星はよく照り返すので明るく見えます。反対に真っ黒な星があったとすれば（熱放射を除けば）その星は反射しません。さらにいえば、入射方向と反射方向の特性まで考慮する必要があります。衝効果はそのような方向特性のひとつと言えます。入射方向と反射方向の特性を考慮した “反射率” として、BRDF（双方向反射率分布関数）を使うことがよくあります。

この記事を書き始めたときは、 BRDF を用いて原理的に「火星の明るさ」を計算しようと思っていたのですが、データが得られず断念しました……。その代わりに、Pythonの天文学ライブラリ skyfield で実装されている mars_magnitude() という関数を参考に、位相角を用いて計算してみましょう。

def mars_magnitude(alpha, r_ms, r_me):
    r_mag_factor = 5. * np.log10(r_ms) # 太陽と火星の距離の項
    delta_mag_factor = 5. * np.log10(r_me) # 地球と火星の距離の項
    ph_ang_factor = 2.267E-02 * (alpha*180/np.pi) - 1.302E-4 * (alpha*180/np.pi)**2
    return -1.601 + ph_ang_factor + r_mag_factor + delta_mag_factor

ここで重要なのが ph_ang_factor という項です。等級が位相角の2次式で近似されており、位相角0（満月みたいな位置）に近づくほど急激に明るくなるように決められています。もう少しここを深掘りしてみたかったけど断念…！詳しい人がいらっしゃいましたら元論文とか教えてください。

結果

以上を元に、「予想される火星の明るさ Mag」「地球と火星の距離 r」「火星の位相角 α」をプロットしてみました。

「r が小さいほど Mag は小さい」「α が小さいほど Mag は小さい」はずですが、いかに……！

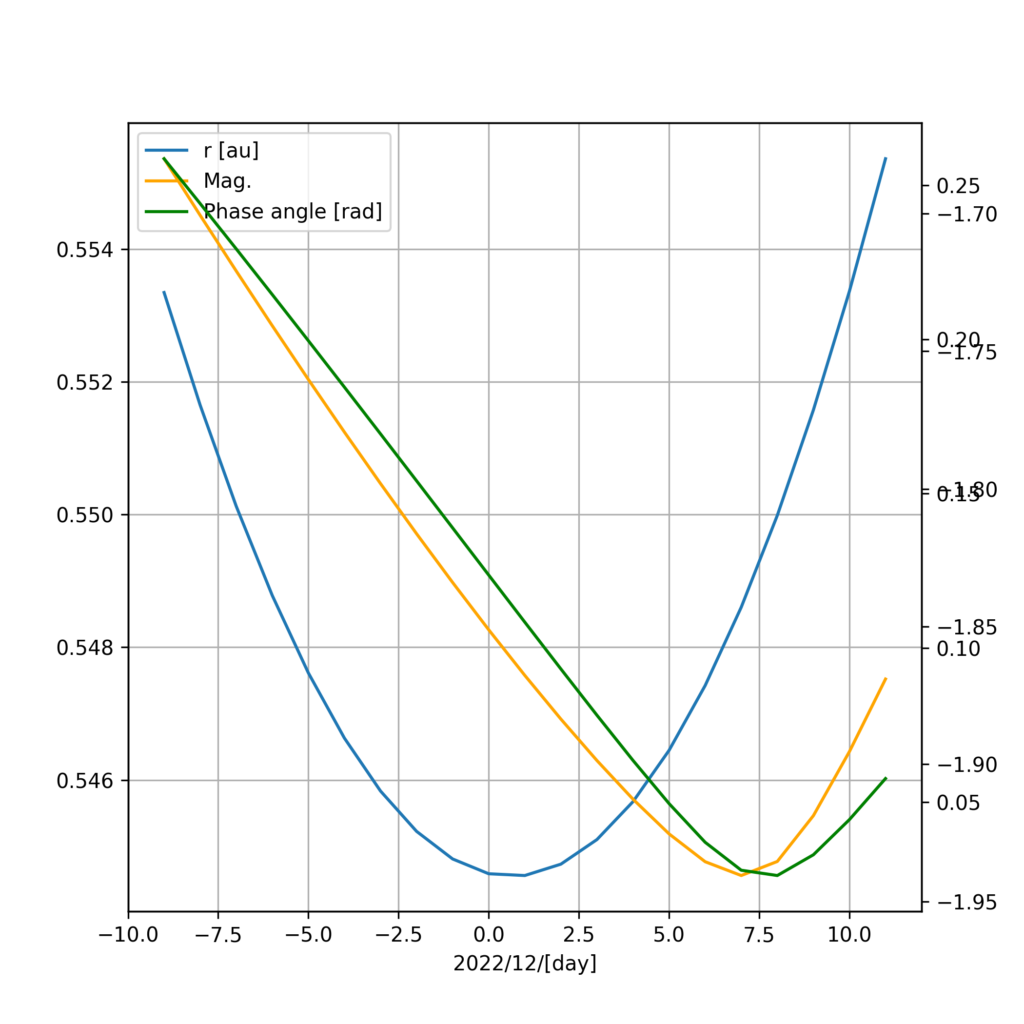
オレンジが明るさ、青が距離、緑が位相角です。（タテ軸の目盛りは心の目で読んでください……！科学者としてはだめです）

明るさのカーブが位相角のものに近いことがわかりました。ピークが少し位相角のものより早いことから、距離による影響も効いていそうですね。

そしてそして！「マイナス1.9等からマイナス2.0等まで」明るくなるというのもそんなに悪くない精度で確認できました¹。

おわりに

まず締め切り大遅刻してすみません……次の日のアドベントカレンダーが公開されてるよね……各位申し訳ありません。

今回は火星の軌道と明るさを計算してみました。たのしかったです（小並感）

私もだけどすごく “師走” 感が出てきましたね。皆様もお変わりなきよう。それでは！

執筆者紹介

執筆：おさむ

URL：https://einstein-cross.com/