
本記事は、天文同人サークル・アインシュタインクロス主催の「天文アドベントカレンダー2022」13日目の記事です。
こんばんは、夢見りあむおさむです!
みなさんはぶっちゃけ冬は好きですか? 僕は微妙です! 寒いのは平気、むしろ好きですが、夜が長くてめっちゃ病むからです1!
今日は全国の病むちゃんに朗報です!
もう日没時刻は遅くなり始めてるそうです
つい先日、このようなツイートをみかけました。
地球はもうだめですのやつやん
日の入りが1年で最も早いのは12月6日だったそうです。マジ……? 冬至まだだよ?(12/13投稿予定でした)
昼の長さでいうと冬至が一番短いけれど、日の出は1月が一番遅いからこんな感じになるそうです。 正午を軸に、日の出日の入りの時刻が対称になっていると思っていたので驚きです。そういえば、部活の朝練に参加していた中学生時代に「なんか朝夕の長さがおかしいな」と疑いを持った記憶がありますが、突き詰めて考えたことはありませんでした。
私はフレックス勤務のため起きるのが遅く、朝早くから太陽が昇っていてもあまり関係ありません。私にとっての「日照時間」は日没時刻と直結しており、日没時刻が遅いほどメンタルに良いです。
いやもう本当に、日没時間が遅くなってきているの嬉しい……‼️ ❤️太陽❤️もっと顔出して❤️(うちわ)
なぜそんな不思議な現象が起きるのか
「冬至より前に、日の入りが一番早くなる」のはなぜでしょうか?( “The Day with the Earliest SunSet comes before the Winter Solstice” の頭文字をとって、今後は “DESS<WS” と呼びます。反対に、日の出の一番遅い日が冬至より後にあることを “WS<DLSR”と呼びます。)
まずは調べることなく、自分の頭だけで説明を試みました。説明できる自信がちょっとあったからです。というのも、もともと大学院でこういう幾何学チックな天文学の理論研究をしていたためです。しかしあいにくその晩はビール3杯焼酎2杯を飲んだ日。29歳の酔っ払いは的外れなアイデアを浮かべては棄却を繰り返すばかり。全然ダメだ〜。回っていたのは頭でも地球でもなくてアルコールでした(カスのLove so sweet)。せっかくなのでそのアイデアを紹介アンド棄却していきましょう。
酔っ払いながら考えたこと① 東京と標準時子午線の経度差
東京は東経およそ140度に位置し、日本時間の基準である東経135度(兵庫県明石市を通っています)から東に5度ほどずれています。この経度差により、単純に考えると、東京の日の出日の入り時刻は東経135度の町と比較して20分ほど早くなっています。少なくとも中学生の私がぼんやり考えたような「正午をはさんで線対称」にはなりません。このせいでずれが生じるのでは?
そこで兵庫県明石市の日の入り・日の出時刻を調べてみました。
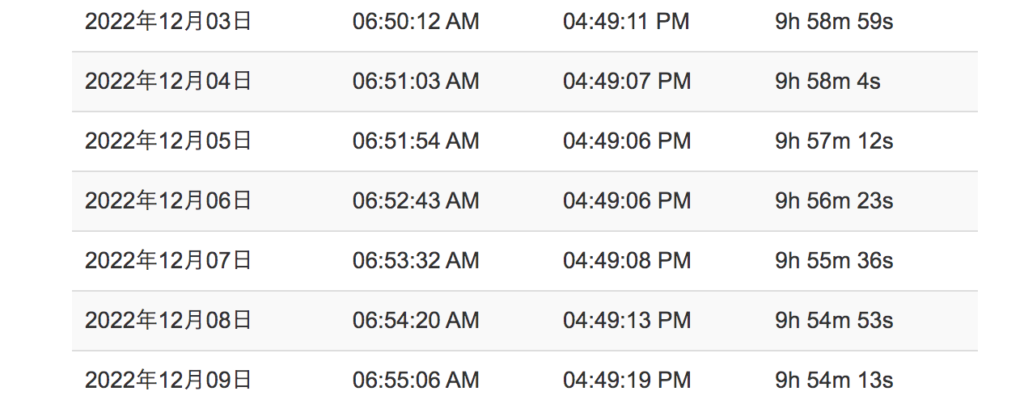
明石市でも同じく DESS<WS となるようです。よって経度差では説明できません。
よく考えれば、明石と東京で20分ほど日没がずれたとしても、どちらの街でも DESS<WS であることに変わりはありませんね。
酔っ払いながら考えたこと② うるう日の存在
1年の長さはぴったり整数日ではなく、365.24… 日 と微妙な値になっています。この余りを打ち消すため、ご存知の通り4年に一度うるう日が挟まれることになっています2。その辺の数値の積み重ねでたまたま今年起きたのかな、いつもは違う日に起きたりするのかなと考えました。
では、去年のDESSを調べてみます。
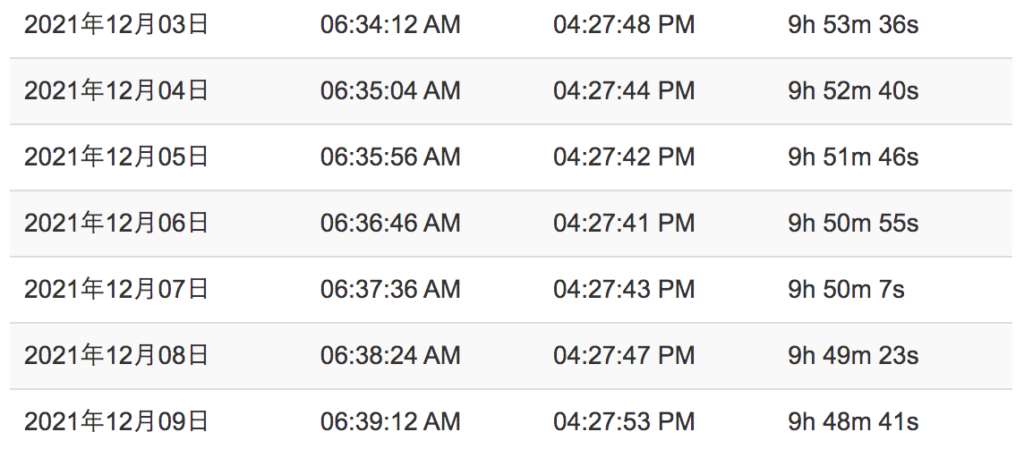
やっぱり12月6日が一番早い……!うるう日は関係なさそうです。
酔っ払いながら考えたこと③ 地球の楕円軌道
地球は厳密な円軌道ではなく、わずかに楕円軌道を描いています。このことが影響するのではと考えました。後で説明しますが、楕円軌道が影響するという仮説は部分的に合っていました。
答え合わせ:アナレンマと均時差
リプ欄と引用ツイートから答えを探しました(酔っ払いは我慢と物理ができない)。
どうやら、「アナレンマ」と呼ばれる現象と関係が深いようです。
アナレンマ(Analemma)とは、均時差によって1年のうちに太陽の位置が8の字型を描いて運動すること。
アナレンマ – Wikipedia

写真は東方向の太陽の位置を年間通じて撮影したもの。うっすら描かれた矢印の方向に年変化していきます。右下が冬至の日の太陽です。8の字を描くため、その幅のぶんも考慮すると、「冬至よりすこし後に、日の出が一番遅くなる」ようです。一方の日の入りは、この8の字が時計回りに西の空に移動していくため、「冬至より少し前に日の入りが一番早く」なります。
ほう…… では、均時差とは?
均時差(きんじさ、equation of time)とは、天球上を一定な速さで動くと考えた平均太陽と、視太陽(真太陽)との移動の差。
(筆者中略)
均時差が変化する事は、視太陽の赤経増加率が一定でない事を意味するが、その原因として次の2つの要因がある。
・地球が楕円軌道を描いて太陽をまわることにより季節によって公転の角速度が異なる。
・赤道が地球の軌道と23°27′傾いている(地球から見ると黄道が天の赤道に対して傾いている)。そのため、太陽が黄道上を等速で動いても(黄経増加率が一定)、赤経の増加率は季節によって変化する。
均時差 – Wikipedia
DESS<WSを引き起こしているのは、「楕円軌道」と「地軸の傾き」のようです。
太陽日と恒星日
私たちの地球は、自転しながら、同時に太陽のまわりを公転しています。つまり、以下の絵のようになっています。
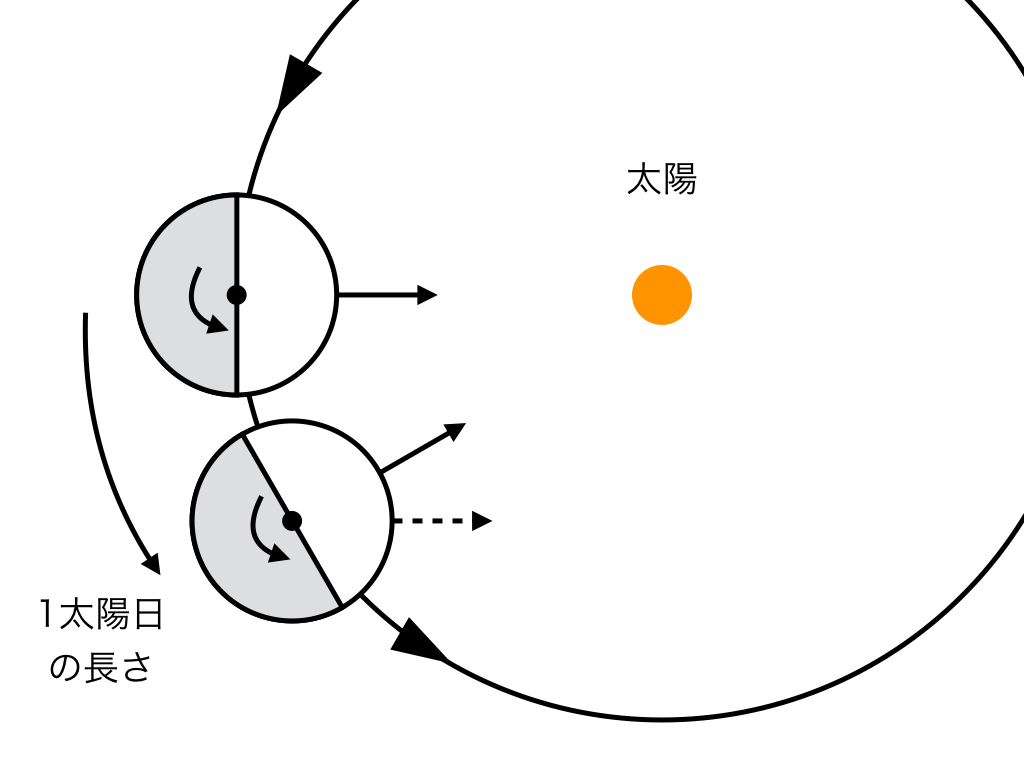
地球が360度自転したあとには、太陽はもう同じ方向(下の図の点線矢印方向)にはいません。もう少し自転を進めて太陽の方向をちゃんと向いた時、やっと1日の長さになります。こうやって定義される1日を「太陽日」と呼びます。私たちに馴染み深い「24時間」という1日は太陽日をもとに定められています。
これに対して、「地球が厳密に360度自転する時間」を恒星日と呼びます。天球の星々に対して1回転する1日なのでこのような名前が付いています。こちらは太陽日より少し短く、23時間56分程度です。
太陽日の伸び縮み
上のポンチ絵では簡単のため、円軌道、地軸の傾きがない場合を描画しました。これは実際の地球よりかなりシンプルにしています。実際の地球では楕円軌道、地軸の傾きがあるため、太陽日は日々変化し伸び縮みします。
軌道計算を実施してアナレンマを観察する
pythonを使って惑星の軌道を計算してみます。使う数学は「三角関数(自転)」と「ケプラー方程式(公転の楕円軌道)」のみです。それ以外の難しい効果(歳差とか相対論的効果など)は入れません。
軌道計算をすることで、架空の惑星でもシミュレーションすることができます。惑星の軌道パラメータを変えて遊んでみましょう。
前回の記事では、火星の見かけの位置を軌道計算によりプロットしてみました。同じコードを使い回す予定でしたが、構造が違いすぎるため断念。スクラッチで書き直しました。
それでは、楕円軌道と地軸の傾きがどのように影響するか調べましょう。視覚的にわかりやすいのでアナレンマをみていきます。
import numpy as np
from planet import Planet, Position # 今回のコードの本体
if __name__ == "__main__":
planet_params = {'name': 'Earth_0_circ', # 惑星の名前をつける
'zeta': 0, # 自転軸傾斜角
'e': 0, # 軌道離心率
'peri': 0, # 近日点黄経
'f_spin': 1+1/365.25, # 自転周波数 [1/day] (恒星日)
'f_orb': 1/365.25} # 公転周波数 [1/day]
position_params = {'name': 'Tokyo', # 観測地点の名前
'lat': +35.6581, # 観測地点の緯度
'lon': +139.7414, # 観測地点の経度
'time_zone': +9} # 観測地点の標準時
earth = Planet(planet_params) # Planet インスタンスの生成
tokyo = earth.at(position_params) # Position インスタンスの生成
days_from_equinox = np.array(range(0, 360, 15)) # 春分を起点に15日おき
tokyo.plot(days_from_equinox, 16.5, 'Western') # 16時30分に東京から西の空を観望するなんか前から思ってたんですけど、コード貼っ付けても映えないですよね。今回は中身まで書きません。
円軌道、地軸の傾き無し
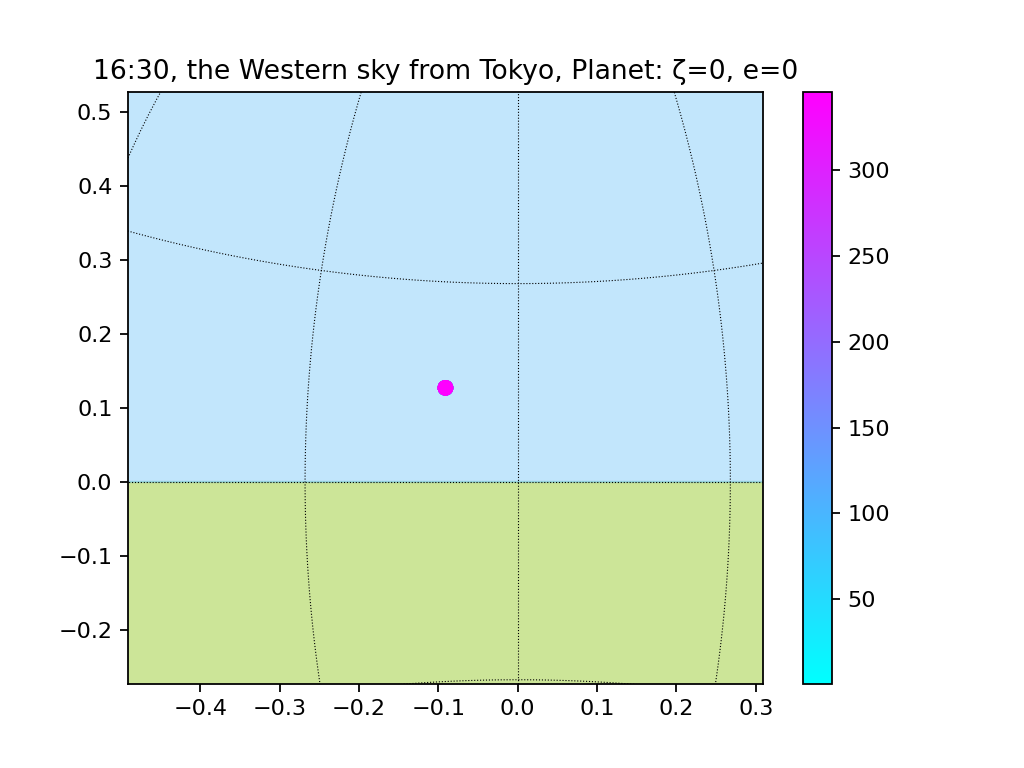
円軌道、地軸の傾きあり(15度、30度、45度)
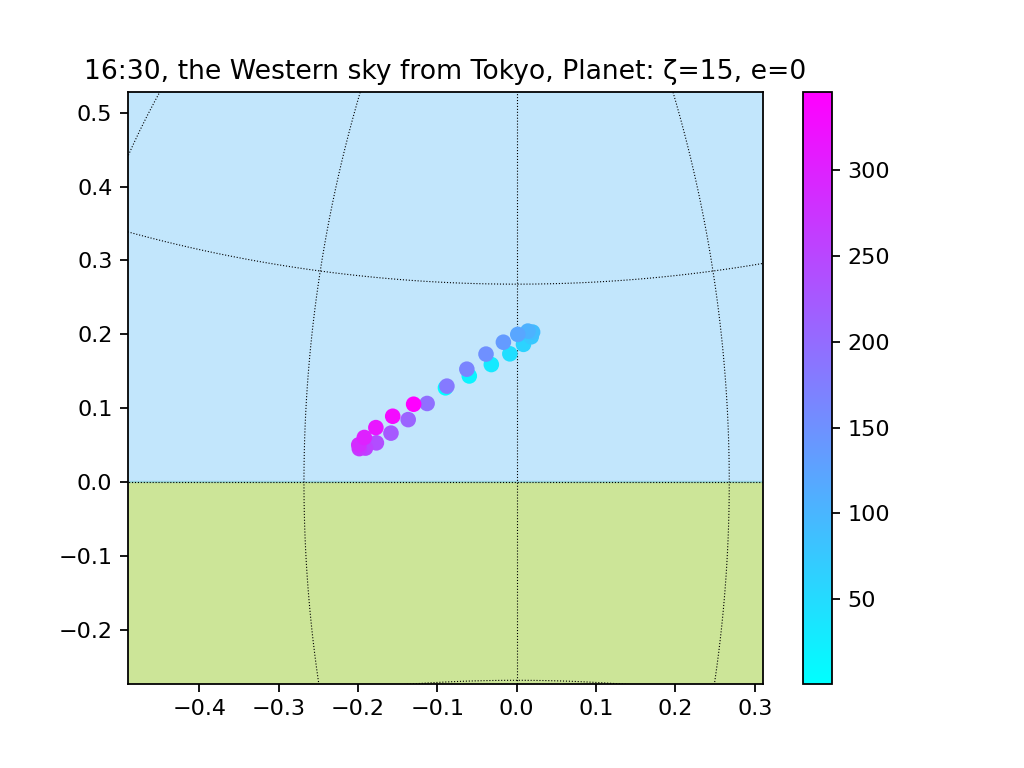
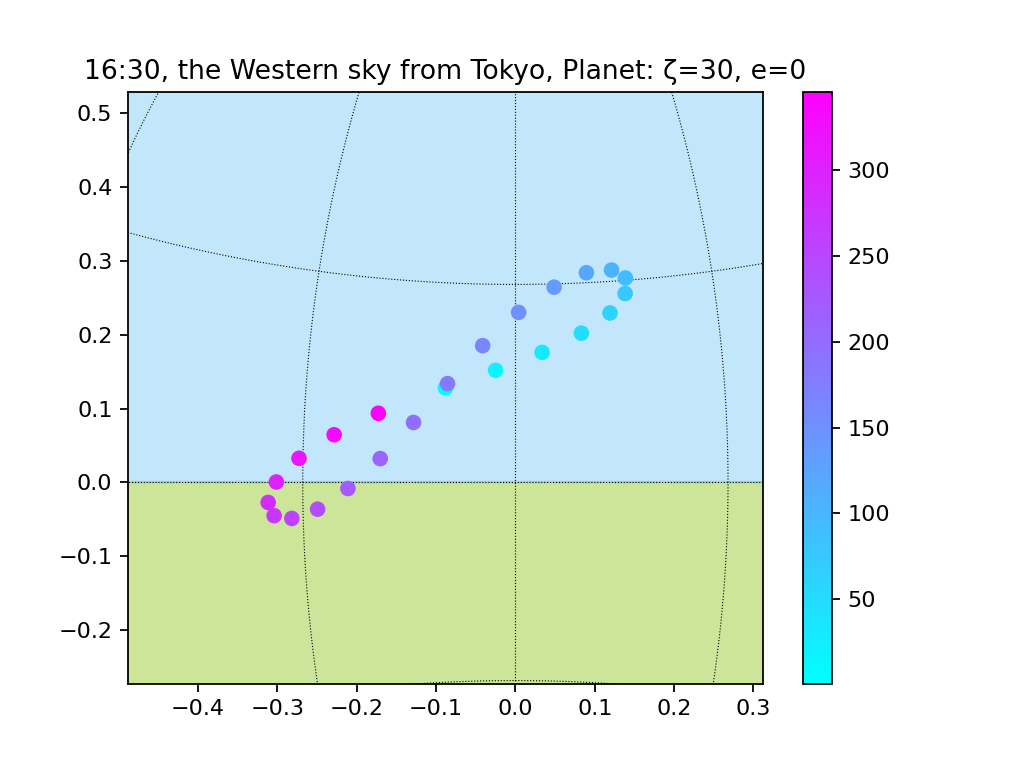
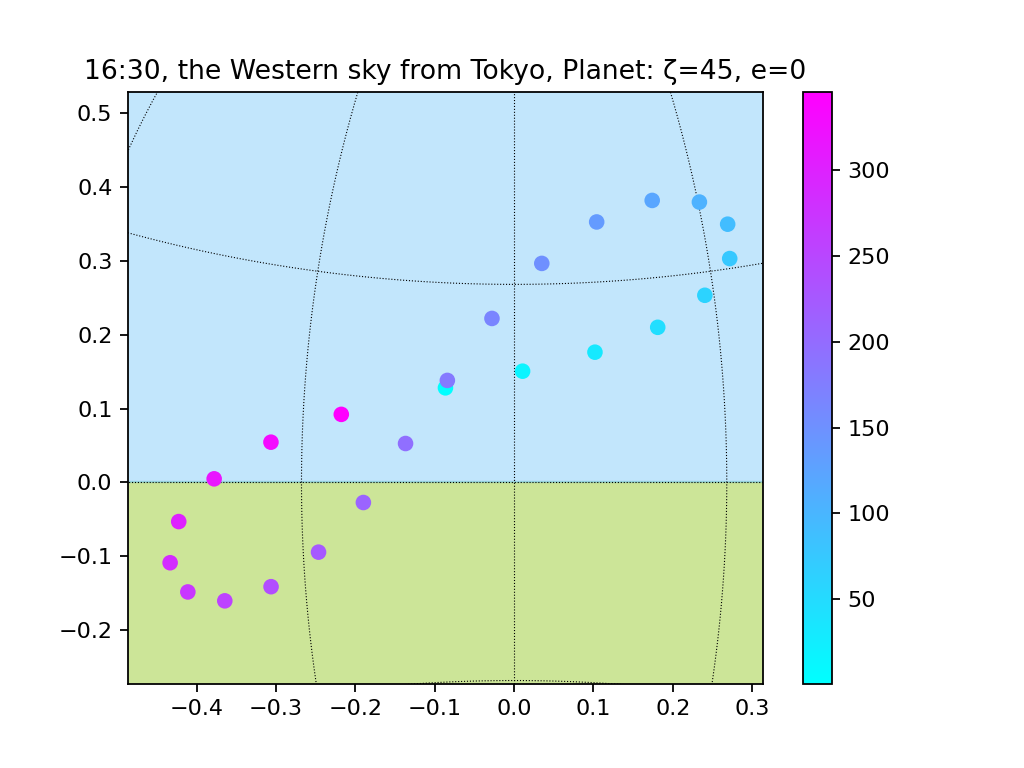
地軸が大きく傾くにつれ、8の字は大きくなるようです。
楕円軌道(e=0.01, 0.1, 0.2)、地軸の傾き無し
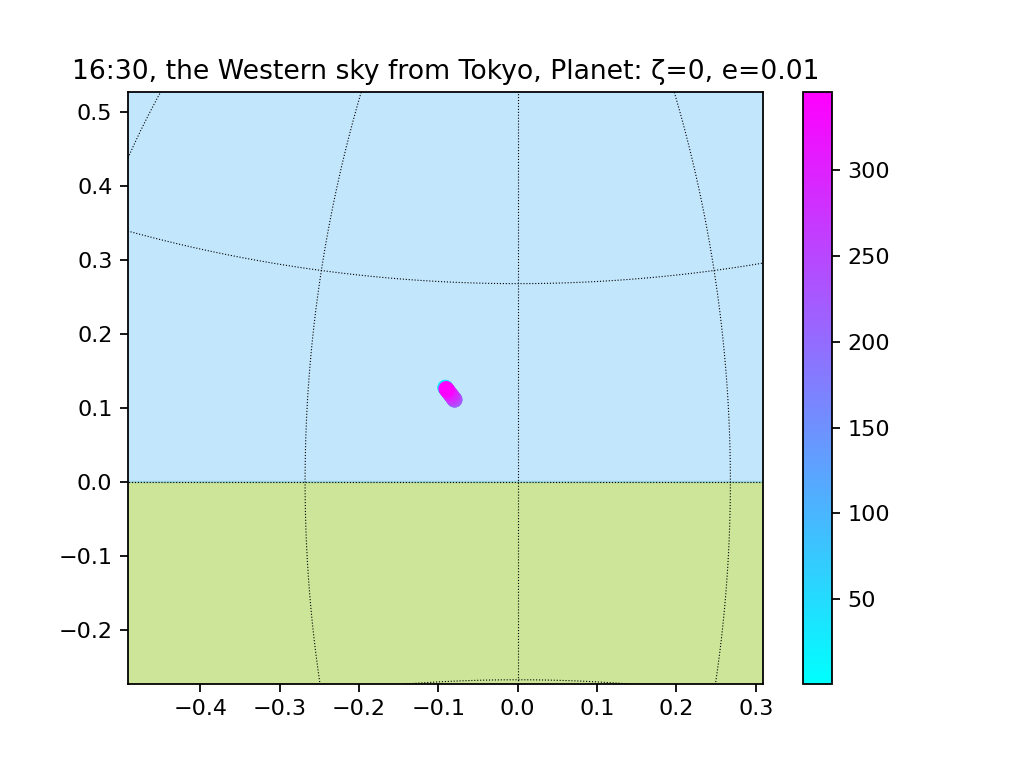
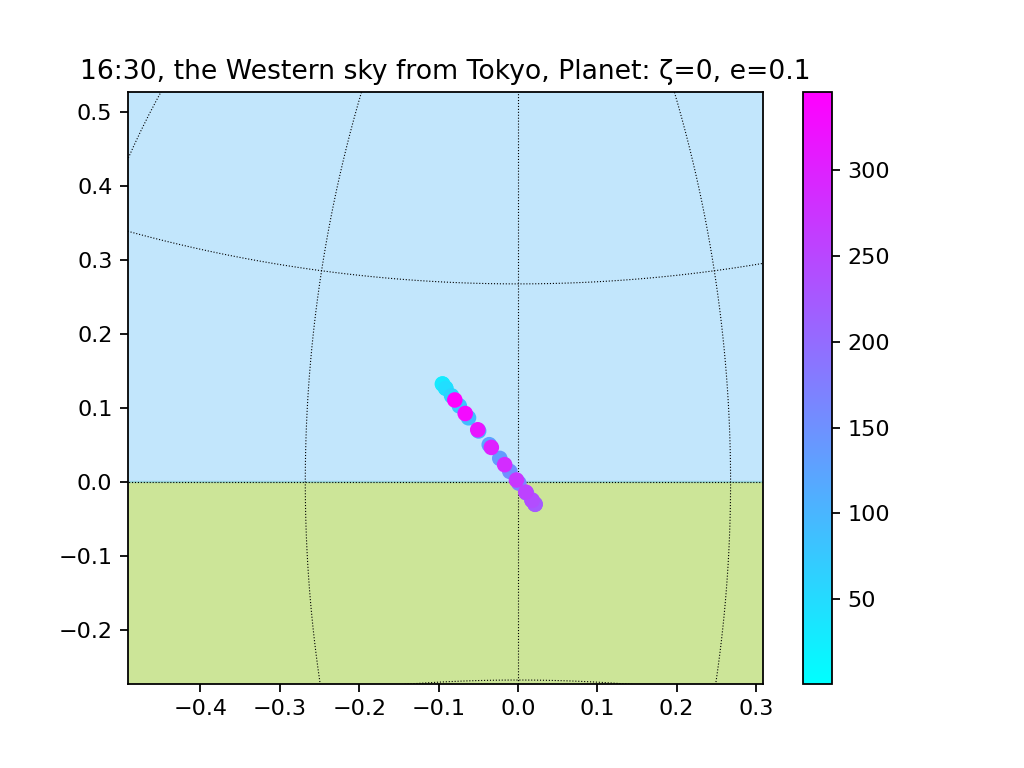
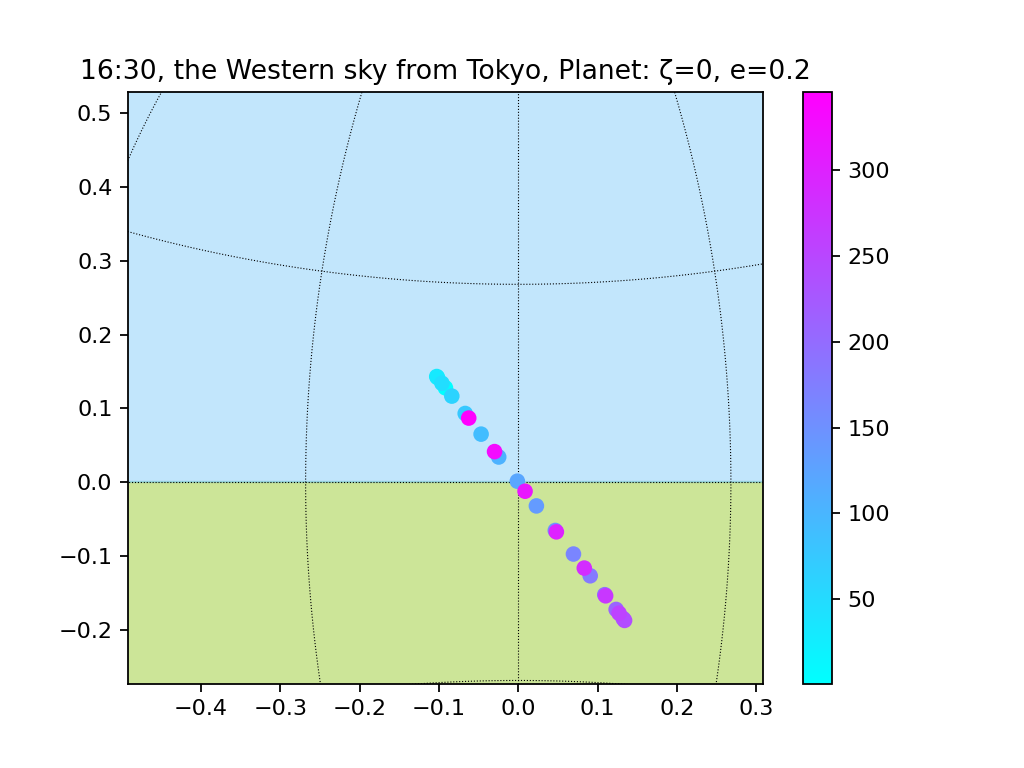
おまけ:観測地点を変えてみる
赤道直下と北極で太陽を観測してみます。
まずは赤道直下。
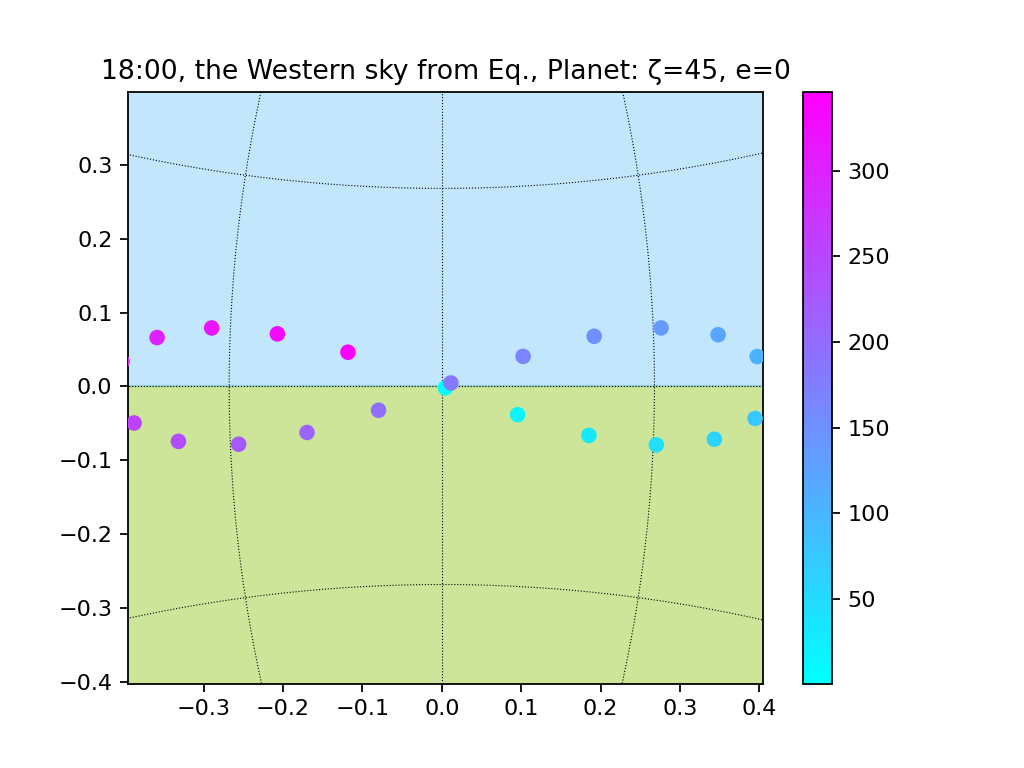
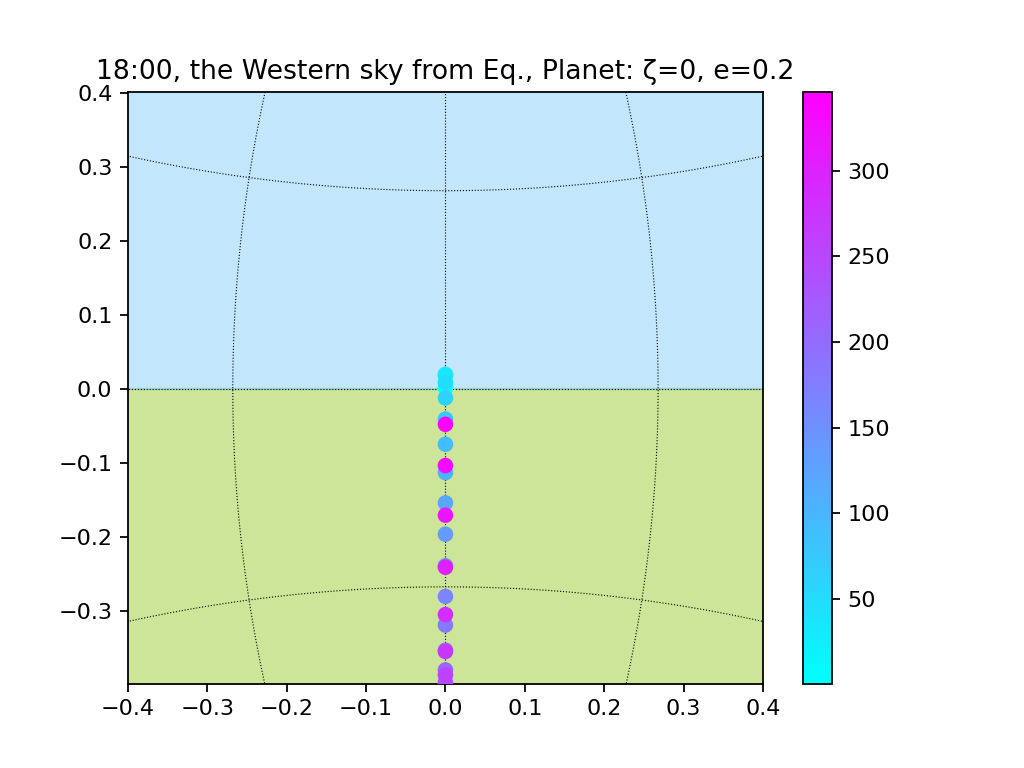
続いて北極。
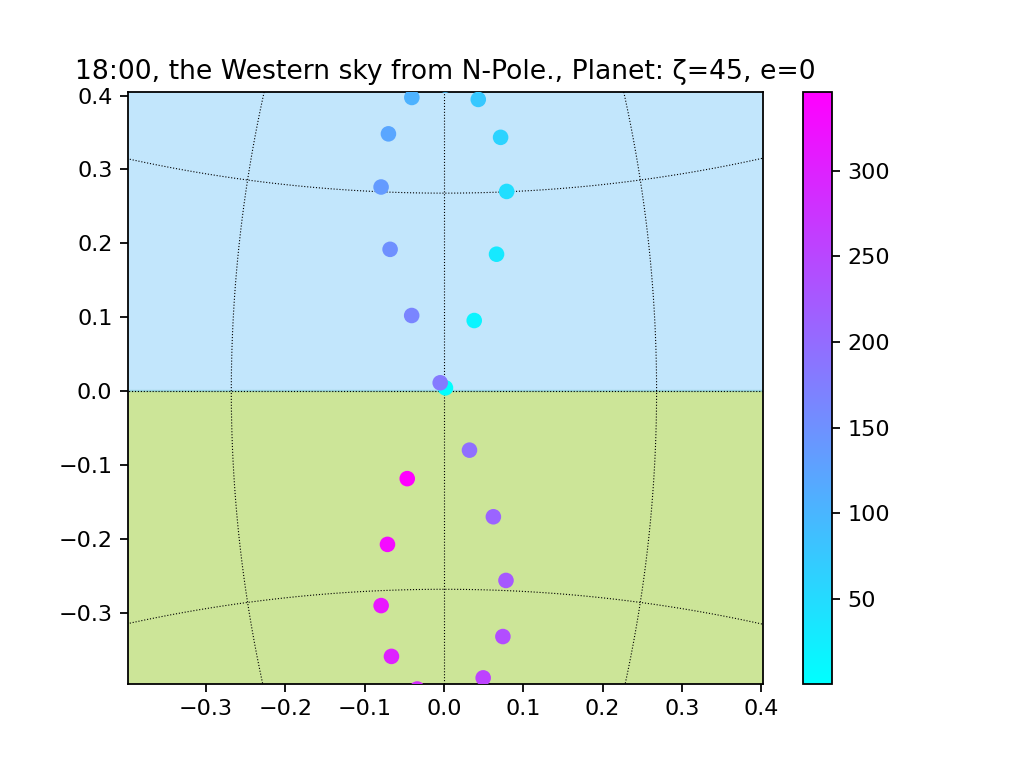
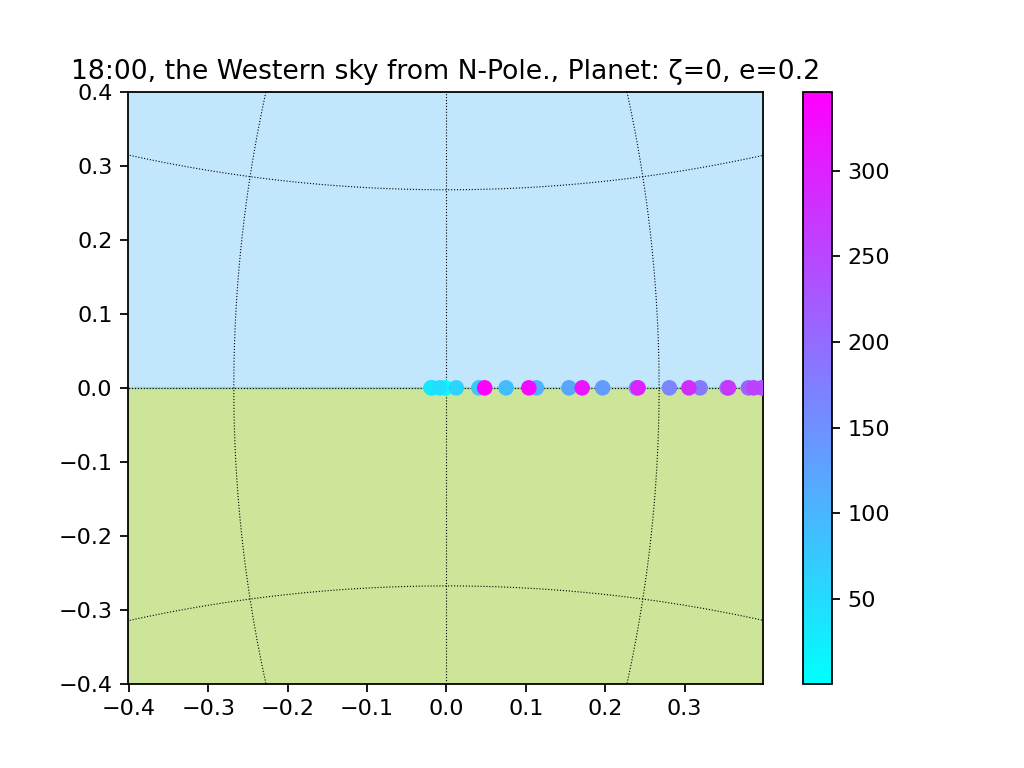
楕円軌道、地軸の傾きあり
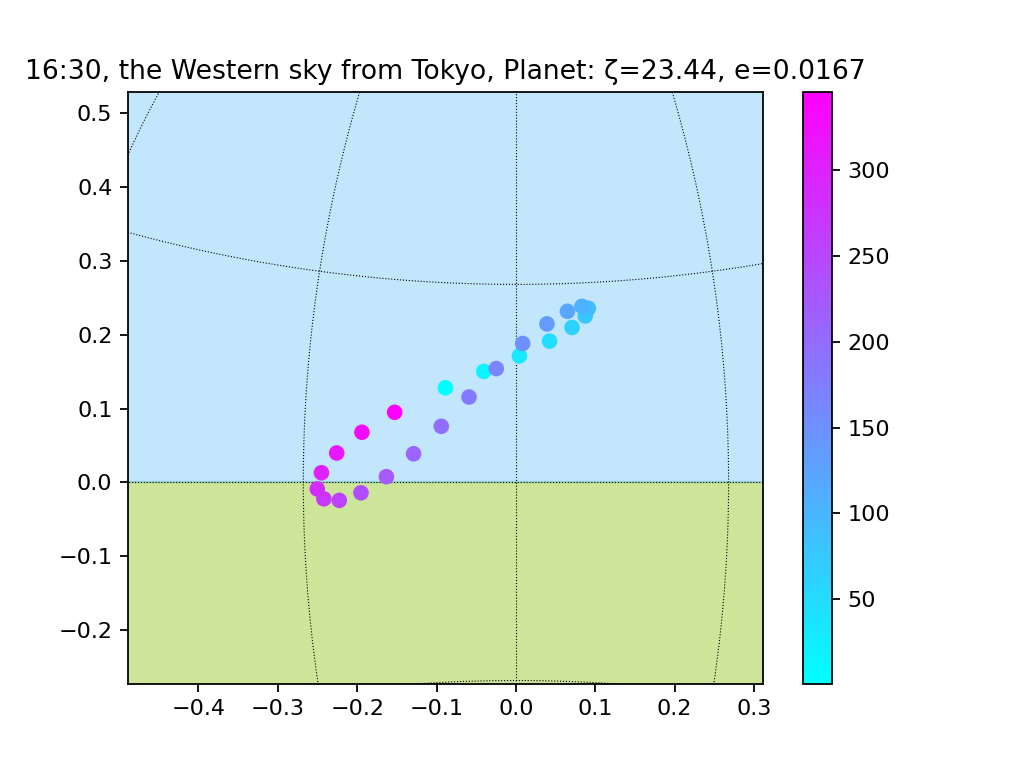
最後に、実際の地球のパラメータ(zeta=23.44、e=0.0167、longitude_peri=-71.853)に合わせてみます。
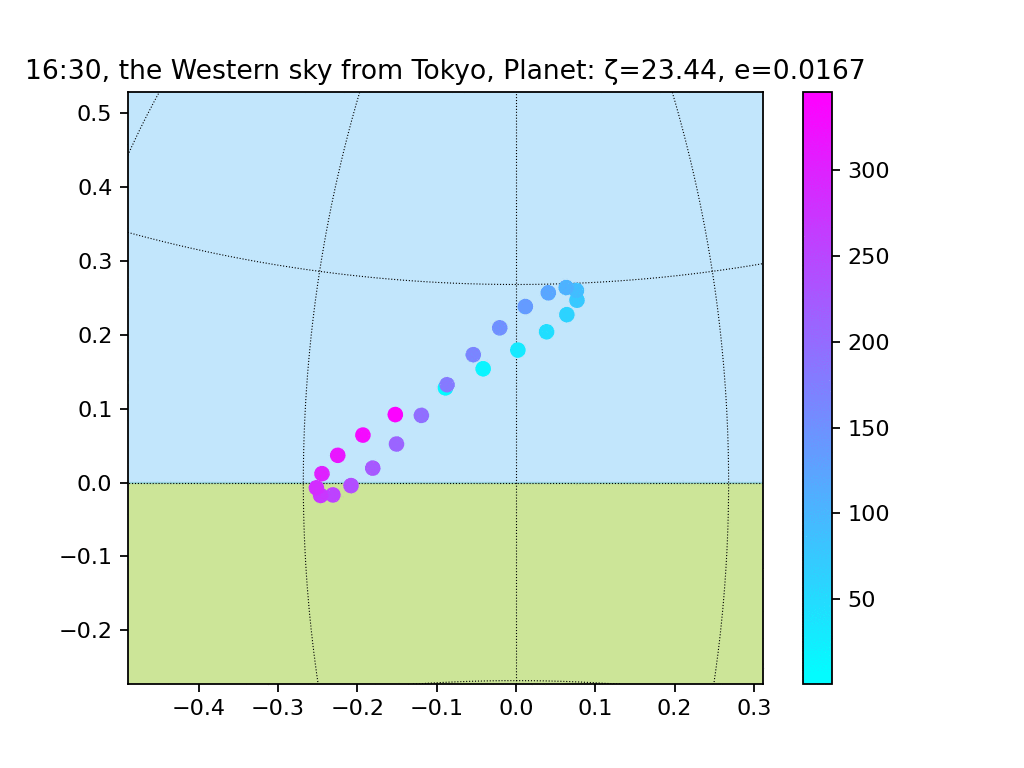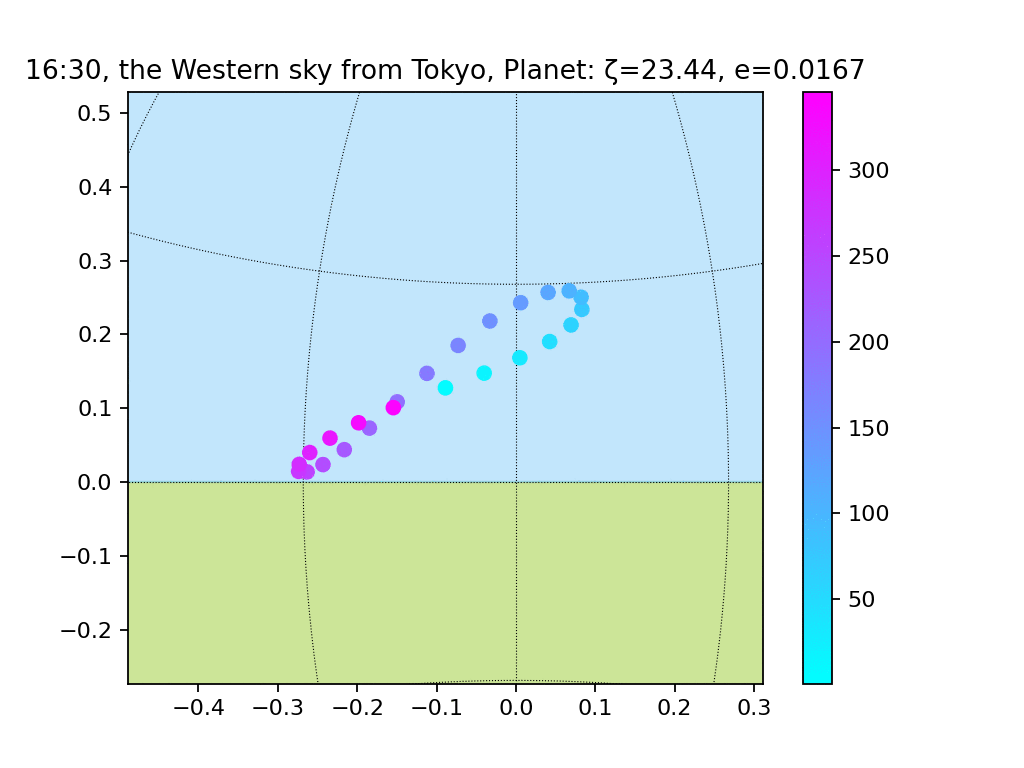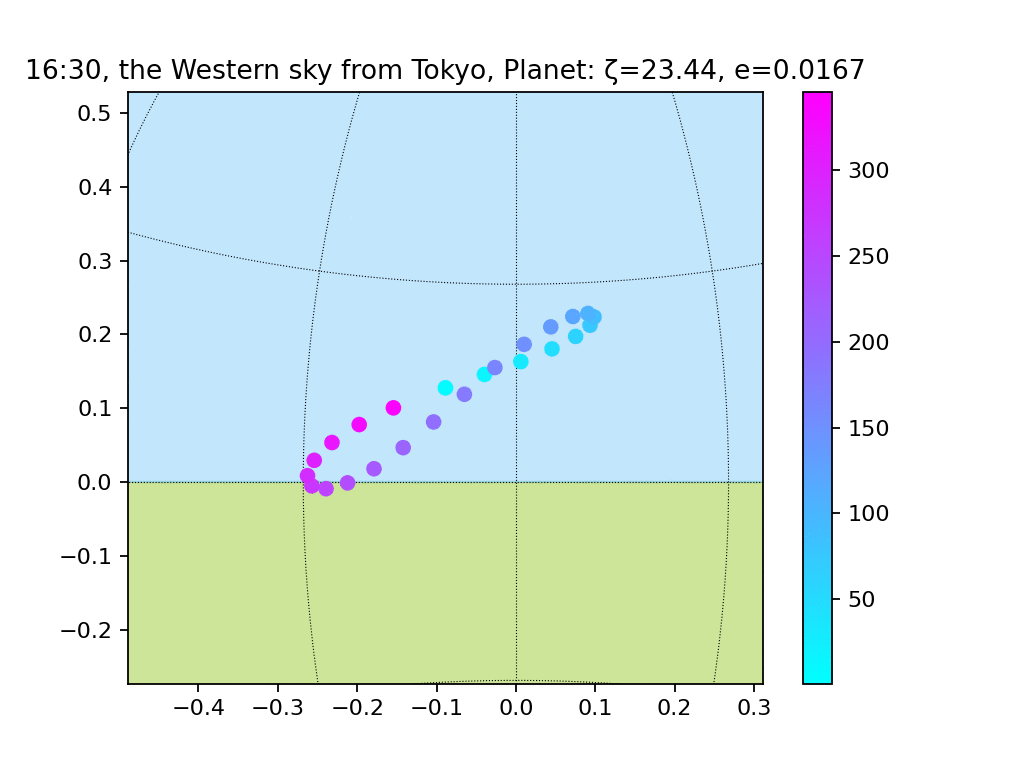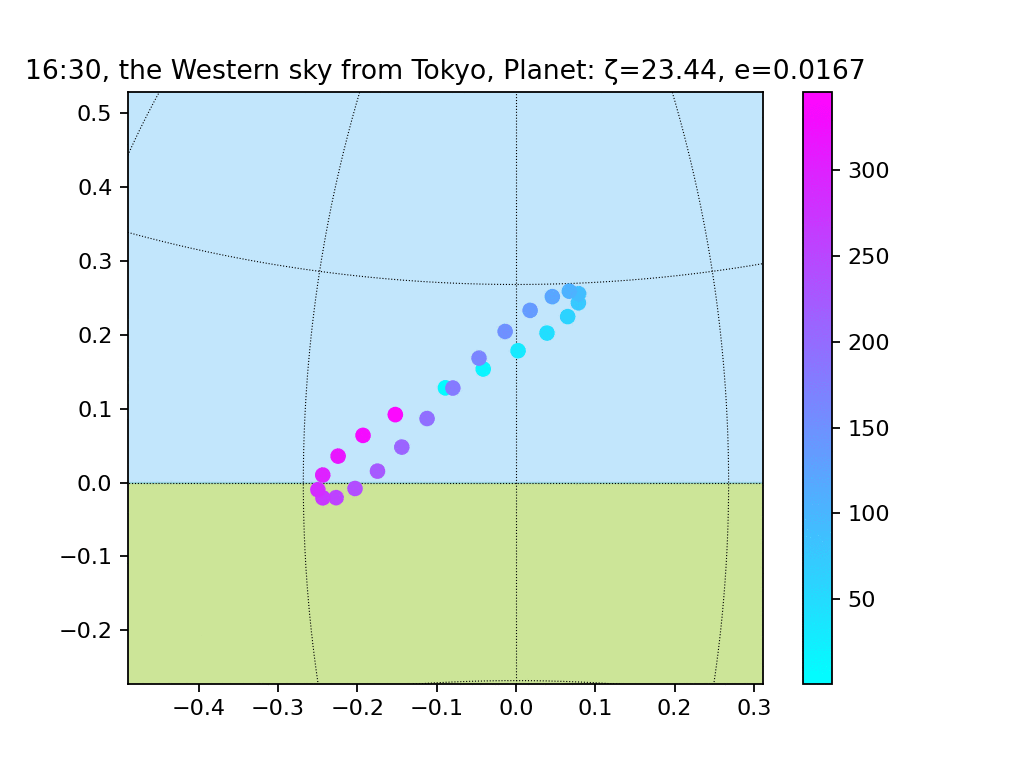
おまけ:近日点黄経を変えてみる
近日点黄経は、春分点方向と楕円軌道の近日点方向の間の角を表すパラメータです。公転角速度が増減するタイミングは近日点黄経によって変わります。したがって、近日点黄経を変えると8の字の形が変化します。なぜかここだけgifを用意してある。
日没時刻について
ここまで、惑星のパラメータと観測地点のパラメータを変えてアナレンマを見てきました。では本題、日出時刻と日没時刻を調べます。アナレンマは、年を通してある時刻に観測し続けた太陽の位置変化を表します。逆に、アナレンマの各点について少し時を戻したり進めたりすれば日出または日没のタイミングがやってきます3。
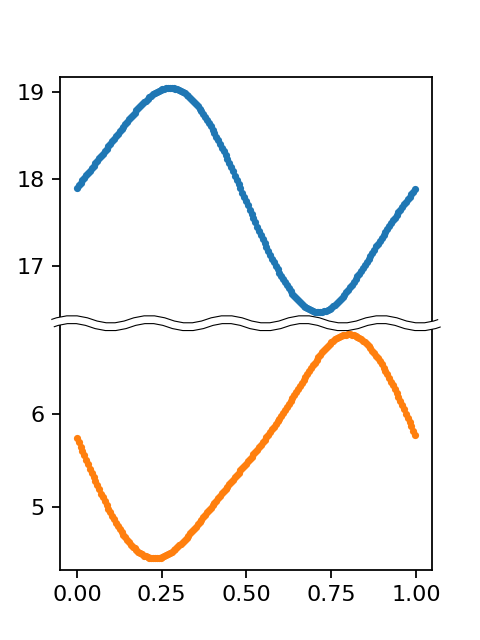
横軸の0.75(〜冬至。楕円軌道を描くため丁度とは限らない)の前後を見ると、日没時刻の極小と日出時刻の極大のタイミングがずれていることがわかります。
定量的にも、元ツイートが示す日没時刻と比較して誤差2分の範囲に収めることができました。最後に、元ツイートっぽく冬至前後3ヶ月に注目してプロットすると、
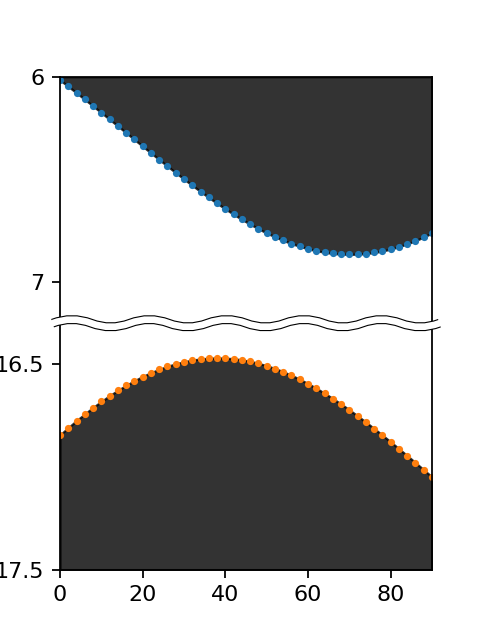
おわりに
本日は均時差とアナレンマという現象を数値解析によって確かめ、「冬至よりも日の入りが早い日がある」ことについて議論しました4。それは地球が持つ「楕円軌道」「地軸の傾き」という2つの性質が引き起こすものです。
今回の調査で私は「こんなにシンプルなのに直感に逆らう現象がまだまだあるなあ」と感じました。
それでは皆様、よいお年を! 来年のアドベントカレンダー(未定)は計画的に執筆します!
執筆者紹介
執筆:おさむ
URL:https://einstein-cross.com/



コメント