はじめまして、おさむです。
天文アドベントカレンダー（day.6）ということで、本記事では
「在野でも楽しく、天文の研究ができるぞ！」
ということをお伝えしたいと考えています。
その研究テーマに選んだのがこちら、「星空の角度相関関数」です。
動機：ランダムな中に見出だす規則性
本研究は、数年前から温めていたアイデアに基づいています。
そのきっかけはこちらのNewtonさんのツイートでした。
直感的には、左がランダムだと思ってしまいますよね。（この記事の読者はよく訓練されているでしょうから、右しかランダムに見えない人も多いかもしれません。）
人は、この右の、真に「ランダム」なパターンから意味を読み取ってしまうものです。私にもなんだか人の形のようなものが見える気がします。
それは、大空の星々の並びに意味を見出し、星座を作り上げていった古代の人々と同じように。1
課題：はたして星空はランダムか？
有史以来、人間はこの肉眼のみで夜空を見つめ続けてきました。夜空に光るもの、とくに点に見えるものは、大きく分けて「動かないもの」と「自由に動き回るもの」があります。それぞれを「恒星（fixed star）」「惑星（planet）」と呼びました。恒星たちはいつも同じ並び方をして──まるで「天球」という面に貼り付けられたかのように──空を巡っていきます。古代の人々は「いつも変わらない星空」と「動き回る太陽と月、そして惑星」の関係に物語を見出し、宇宙観や神話を構成してきました。
そう、恒星だけに。
なんて冗談は置いておいて、オリオンの砂時計のような配置や腰の三つ星を見ると、確かに私だって「誰かがそこにそう配置した」2のではないかと思えてきます。
時代が下って科学と技術が進歩し、いまや私達は、惑星が太陽の周りを巡っていること、天球面などなく奥行きがあって、目に見える星々は同じ天の川銀河に属する星のうち6等より明るい (
近傍の) ものだけだったこと、そもそも天の川が星の集まりだったことを知っています。”fixed”と呼んでいた恒星も、人類の時間スケールに比べれば長いだけで運動をしています。
話をもとに戻しましょう。人々は古代から星の並びに意味を見出してきました。しかしその星々は、「神が何かのモチーフを描いた」ものではないのです。かといって、「重ならないよう配置」したものでもなければ、「まったくのランダム」でもないと想像できます。なぜなら星々は、重力的・化学的な自然法則に従って共に進化してきた存在だからです。
ではどのような並び方をしているか？ 以下の2点は筆者が予想した「星の並びの傾向」です。
- 我々は天の川銀河の中にいるので、近所の星はほとんど等方的（ランダム）だが、銀河面に沿った分布も見られるかもしれない。
- 連星があるため、2星間の距離が近いものが肉眼でも多数観測されるはず。
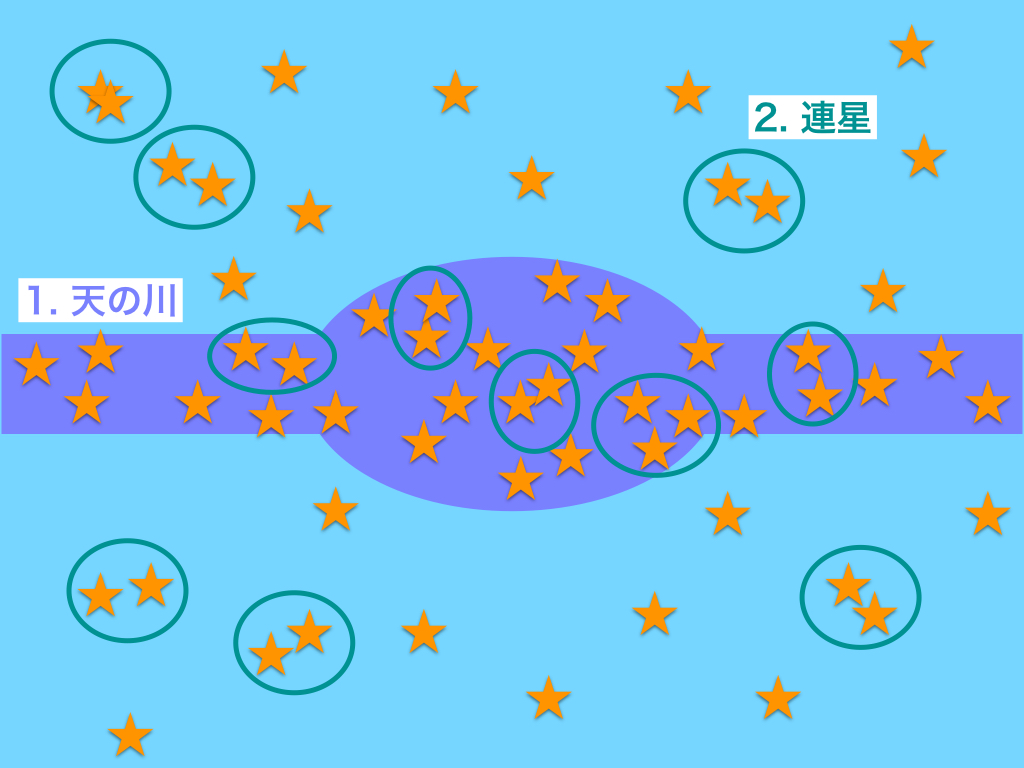
予想した物理的効果をもとに、星の分布をちょっと極端に模式化してみました。
目標：星空の特徴を定性的に理解する
では、本当に星空がランダムでないか、また上の予想が正しそうかを実証していきます。
今回の実証では、「角度相関関数」を用います。
……角度相関関数とはなんぞや？
まずはこの動画を御覧ください。（本題は0:54 ~ ）
角度相関関数は、2点ペア間の距離をカウントすることで、分布の特徴をつかむ手法です。
動画では、宇宙の大規模構造観測データから「バリオン音響振動（BAO）」という宇宙初期に起きた波紋の痕跡を検出するために使われています。その他にも宇宙背景放射（CMB）などでも同じ手法が用いられています。2019年ノーベル物理学賞受賞のJames Peebles博士らの研究は（もちろんこれだけではないですが、）このあたりの初期宇宙に関するものです。
動画では点ペアカウントのヒストグラムを見ていましたが、本研究の評価は
を用います。 
は星と星の距離相関、 
はランダムにまいた点同士の距離相関です。
は何割増しかを表す量なので、正ならばランダムな場合に比べ多く分布し、負ならば少なく分布していると言えます。
下の図の太い青線はNewtonさんのツイートのように「重ならないよう配置した」星々の、細い赤線はランダムに配置した星々の の模式図です。
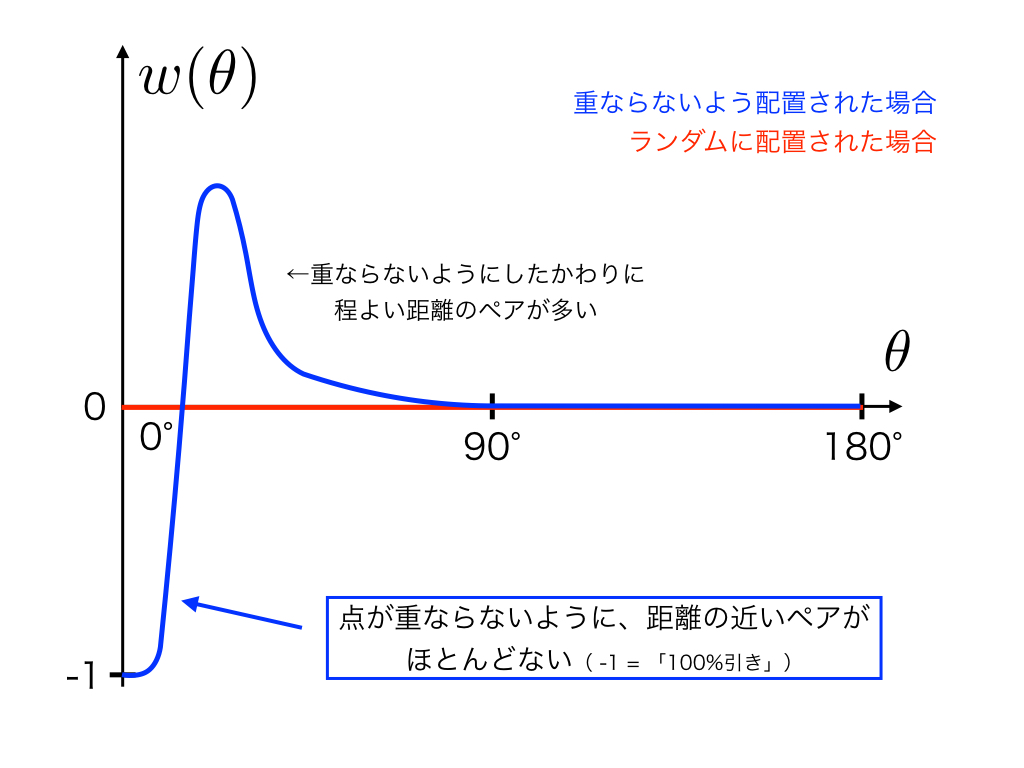
よく接近した点のペアが少なく、そのかわり程よく離れたペアがそこそこいるはずです。（Newtonさんの画像を使った解析がお見せできればよかったですね……！）
本物のデータを使えば、連星の存在により0度近くのピークが、また天の川銀河の影響により未知の効果が予想されます。
さて、実際のデータを用いて解析を行ってまいりましょう。
目視できる（6.00等より明るい）星の位置データはこちらのサイト(star_map.txt)よりお借りしました3。
誤差の評価には、ビン内のカウントのポアソンエラーを用いました4。
星のデータは5044個、ランダムな点は10000個を用意しました。ビンは
を50等分しています。
また「角度」相関関数と言っているように、3次元空間での距離ではなく、天球上の角距離を計算してカウントしました。このようにすることで、観測が難しい星までの距離を使わず、ティコ・ブラーエが肉眼で観測していた16世紀の知識でも解析が可能な範囲になっています。
なお、本研究では解析にpythonを用いましたが、2点のペアの計算をforループで回しているので3分くらいかかっていました。コードの公開予定は今の所ないです。
結果：予想は正しそう！？
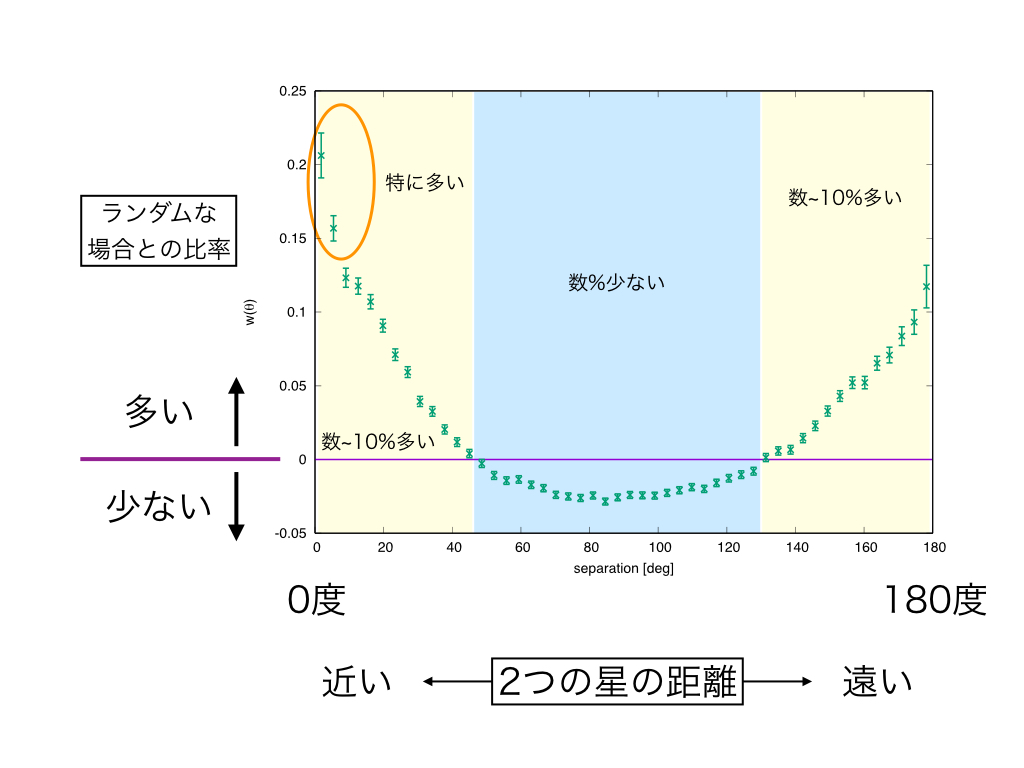
こちらが本研究のメイン結果です。プロットから、
- 角度 0度付近と180度付近がランダムに比べて多い。一方90度付近は少ない。
- とくに角度 0度付近は180度付近と比べても多い。
ことが読み取れます。この結果について考察していきましょう。
まず 2. のほうが簡単で、連星の存在により、見かけの近い星のペアが多く観測されたことが原因だと考えられます。
次に 1. ですが、これも予想した「天の川銀河」というキーワードで説明ができそうです。というのも天の川銀河面上の星は大円状に分布しており、すると天球の正反対側にも星が居やすいからです。
まとめと展望
いかがだったでしょうか？今回は長年アイデアを温めていた「星空の角度相関」を研究してみました。その結果、星の並びがランダムからわずかに離れていること、そして2つの重力的な効果で定性的に説明できることを示しました。研究に用いたデータも簡単に手に入り、解析手法もオープンな範囲から調べて実装できました。在野でも楽しそうな研究ができる！ことが伝わればいいなと思います。5
この研究をやってみて、私はシンプルに楽しかったです（小並感）。
また機会があれば小ネタ研究を紹介しますね！ご覧いただきありがとうございました。
参考文献
科学雑誌Newton（ニュートン）公式 twitter
「アステリズム」Wikipedia
Illustratorで星図と星座を描くスクリプト
Bias and Variance of Angular Correlation Functions
執筆者紹介
執筆：おさむ
Twitter：@036Rmsna
URL:https://einstein-cross.com/
この記事はAstro Advent Calendar 2021の企画記事です。
コメント